Attention is All You Need
Paper-pdf
Authors: Vasvani, et al (Google Brain), arxiv
Hypothesis
Using self-attention (attention that relates to different positions of a single sequence in order to compute a representation of the sequence), without using RNNs or convolution is enough for representing the input. Instead of CNN -> Attention -> CNN they use Dense -> Attention.
Background
Some recent work has tried to reduce sequential computation through use of convolutional networks as basic building blocks, computing hidden representations in parallel for all input and output positions.
In these models, the number of operations required to relate signals from two arbitrary input or output positions grow in the distance between the positions linearly for ConvS2S and logarithmically for ByteNet, making it difficult to learn dependencies between distance positions.
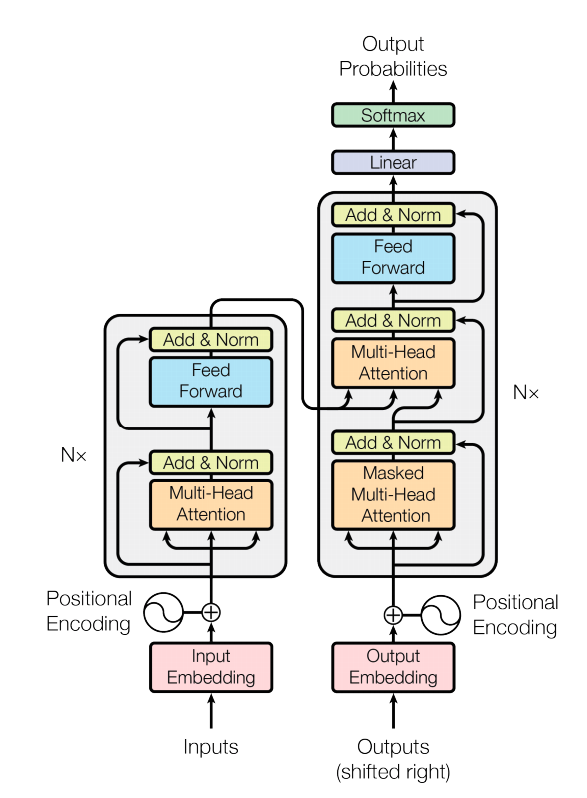
Model Architecture
Their model is called Transformer and follows the general encoder-decoder framework: given an input sequence $(x_1,…,x_n)$ the encoder maps this into a sequence of continuous representations $\mathbf{z}=(z_1,…,z_n)$. Given $\mathbf{z}$ the decoder generates an output sequence $(y_1,…,y_m)$ one element at a time.
- The encoder is a stack of $N=6$ identical layers.
- Each layer has two sublayers
- Multi-head self-attention mechanism
- Position-wise fully connected feed forward network.
-
They employ residual connection around each of the two sub-layers, followed by layer normalization
- The decoder is also a stack of $N=6$ identical layers.
- Each layer has three sublayers:
- Masked multi-head attention to prevent positions from attending to subsequent positions
- Multi-head attention to perform attention over the output of the encoder stack
Attention
An attention function can be described as mapping a query and a set of key-value pairs to an output. The output is computed as a weighted sum of the values, where the weight associated with each value is computed by a compatibility function of the query with the corresponding key.
The query is usually the hidden state of the decoder. A key is the hidden state of the encoder and the corresponding value is the normalized weight, representing to what extent the key is being attended to. The way the query and the key are combined to get a value is by a weighted sum. Here, a dot product of the query and a key is taken to get a value.
scaled dot-product attention:
Softmax of the scaled dot product of the query with all the keys (query dimension: $d_k$, value dimension: $d_v$). The dot products tells you how relevant this input is to the query.
\begin{align} \mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK_T)}{\sqrt{d_k}})V \end{align}
$Q$: matrix of queries. Dot product is much faster and more space-efficient.
Multi-head attention
\begin{align} MultiHead(Q, K, V)=Concat(head_1,…,head_h)W_O \end{align}
where:
\begin{align} head_i = Attention(QW_i^Q, KW_i^Q, VW_i^V) \end{align}
Linearly project the queries, keys, and values $h$ times with different, learned projections to $d_k$, $d_k$ and $d_v$ dimensions.
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.
In the work they use $d_k=d_v=d_{model}/h=64$.
Applications of Attention in the Model
1- In encoder-decoder attention layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence.
2- The encoder contains self-attention layers. Keys, values and queries come from the output of the previous layer in the encoder. Each position in the encoder attends to all positions in the previous layer of the encoder.
3- In the decoder, allow each position in the decoder to attend to all positions in the decoder up to and including that position.
Theoretically, the input and output of each layer are 2-dimensional tensors with shape [sequence_length, d_model]. In the actual implementation, where the authors process batches of sequences, the inputs and outputs are 3-dimensional tensors with shape [batch_size, sequence_length, d_model]
Position-wise feed-forward Networks
Each layer in the encoder and decoder, contains a fully connected feed-forward network, applied to each position separately and identically:
\begin{align} FFN(x) = max(0, xW_1+b_1) W_2 + b_2 \end{align}
Two convolutions with kernel size 1.
Positional Decoding
Since the model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, “positional encodings” are added to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension d-model as the embeddings, so that the two can be summed. There are many choices of positional encodings, in this work, sine and cosine functions of different frequencies are used.
Recap
Replacing convolutional and recurrent encoder, decoders with only attention and dense layers.